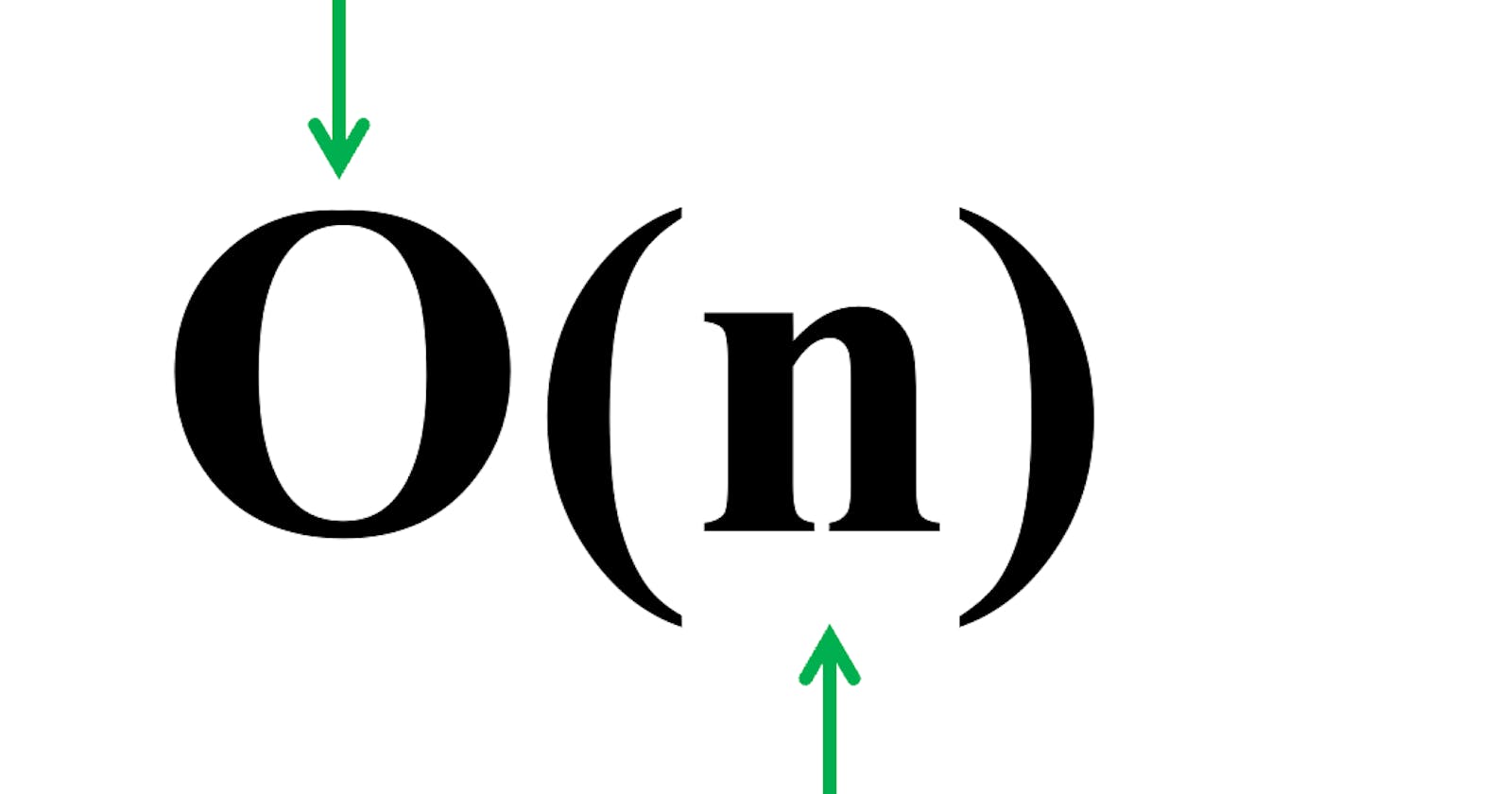Understanding the Almighty Big-O Notation

Big-O Notation is an important concept in data structure and algorithm as it's the metric used to describe the efficiency of an algorithm. It also measures the complexity, whether time or space of an algorithm. Without a proper understanding of Big O, it will be very difficult to judge when your algorithm is getting faster or slower.

Ipso Facto, in this article, we'll be using JavaScript in our examples. I've decided to keep things simple and concise. Now let's get started!

Below are the important terms and keywords to look out for:

Complexity Analysis This is the process of determining how efficient an algorithm is. Complexity analysis usually involves finding both the time complexity and the space complexity of an algorithm. It is also used to determine how good an algorithm is and whether it's better than another one.

Time Complexity A measure of how fast algorithm runs, time complexity is a central concept in the field of an algorithms.

Space Complexity It is a measure of how much memory an algorithm takes up, this is also a central concept in the field of an algorithms.

Rules of Big-O Notation

The main purpose of algorithm analysis is to understand the efficiency of an algorithm by calculating the f(n); it can be tasking and challenging to calculate f(n) and that's why Big-O notation provides some fundamental rules to help programmers compute for f(n).

Let's represent the complexity of an algorithm as f(n) where:

n represents the number of inputs,

f(n)time represents the time needed,

f(n)space represents the space or memory needed to process the algorithm

1. Coefficient Rule: This is the first rule and it eliminates coefficients not related to the input size, n. It simply requires you to ignore any non-input-size-related constants. It's imperative to know that this is the most important rule of Big-O notations.

Now, let's take a look at some examples below:

Example I:

function a(n) {
let count = 0;

for (let i=0; i < n; I++){
count += 1;
}

return count
}

This above block of code has f(n) = n. This is because it adds to count n times. By that very fact, this function is O(n) in complexity which is called linear complexity.

Example II:

function a(n) {
let count = 0;

for (let i = 0; i < n*10; i++) {
count += 1;
}

return count
}

In this example, f(n) = 10n because it runs from 0 to 10n, by applying coefficient rule, which is to eliminate any coefficient; then we have O(n) instead of O(10n). Therefore, just like the first example, this also has a Big-O notation of O(n).

2. Sum Rule: This rule simply states that if a resultant time complexity is a sum of two different time complexities, the resultant Big-O notation is also the sum of two different Big-O notations. Let's not forget to apply the coefficient rule after applying this rule.

Let's take a look at the example below:

function a(n) {
let count = 0;

for (let i = 0; i < n; i++){
count += 1;
}

for(let i = 0; i < 11* n; i++){
count += 1;
}

return count;
}

The above block of codes demonstrates a function with two main loops whose time complexities must be considered independently and then summed.

The first loop has f(n) = n, and the second loop has f(n) = 11n. This results in 12n. However, when applying coefficient rule, the final result is O(n) = n (Linear complexity).

3. Product Rule: From the word product, it states that Big-O is multiplied when the time complexities are multiplied. This simply states how notations can multiplied.

Let's take a look at this example below:

function a(n) {
let count = 0;

for(let i =0; i <n; i ++){
count +=1;

for(let i =0; i < 10 *n; i ++){
   count += 1;
}
}

return count;
}

In the above block of codes, f(n) = 10n n because the second loop runs 10n times for a total of n iterations. Therefore, this results in a total of 10n² operations. Applying the coefficient rule, the result is that O(n) = n².

4. Polynomial Rule: This rule states that polynomial time complexities have a Big-O notation of the same polynomial degree.

Let's take a look at the example below:

function a(n){
let count = 0;

for(let i = 0; i < n*n; i ++) {
count += 1;
}

return count;
}

In the above block of codes, f(n) = n ² because the loop runs n*n iterations.

5. Logarithmic Rule: With the log of a power rule, constants within a function are also ignored in Big-O notation.

Let's take a look at the example below:

function a(n) {

for (let i = 0; i <n; i * 2) {
console.log(n)
}
}

This above block of codes is a logarithmic complexity. For a given n, this will operate only log ₂n times because i is incremented by multiplying by 2 rather than adding 1 as in the other examples.

Conclusion

Big-O is important for analysing and comparing the efficiencies of algorithms. The analysis of Big-O starts by looking at the code and applying the rules to simplify the Big-O notation.

Variables used in Big-O notation denote the size of inputs to algorithms. For example, O(n) might be the time complexity of an algorithm that traverses through an array of length n; Similarly, O(n + m) might be the time complexity of an array that traverses through an array of length n and through a string of length m.

The following are examples of common complexities and their Big O notations, ordered from fastest to slowest:

• Constant: O(1)

• Logarithmic: O(log(n))

• Linear: O(n)

• Log-linear:O(nlog(n))

• Quadratic: O(n²)

• Cubic: O(n³)

• Exponential: O(2ⁿ)

• Factotrial: O(n!)

Note that in the context of coding interviews, Big-O notation is usually understood to describe the worst-case complexity of an algorithm, even though the worst-case complexity might differ from the average-case complexity.

For examples, some sorting algorithms have different time complexities depending on the layout of the elements in their input array. In rare cases, their time complexity will be much worse than in more common cases. Similarly, an algorithm that takes in a string and performs special operations on uppercase characters might have a different time complexity when run on an input string of only uppercase character vs. on an input string with just a few uppercase characters.

With that being said, when describing the time complexity of an algorithm, it can sometimes be helpful to specify whether the time complexity refers to the average case or to the worst case.

Thank you for reading 👏